Real-Time Recognition of Handwritten Chinese Characters Spanning a Large Inventory of 30,000 Characters
AuthorsHandwriting Recognition Team
Real-Time Recognition of Handwritten Chinese Characters Spanning a Large Inventory of 30,000 Characters
AuthorsHandwriting Recognition Team
Handwriting recognition is more important than ever given the prevalence of mobile phones, tablets, and wearable gear like smartwatches. The large symbol inventory required to support Chinese handwriting recognition on such mobile devices poses unique challenges. This article describes how we met those challenges to achieve real-time performance on iPhone, iPad, and Apple Watch (in Scribble mode). Our recognition system, based on deep learning, accurately handles a set of up to 30,000 characters. To achieve acceptable accuracy, we paid particular attention to data collection conditions, representativeness of writing styles, and training regimen. We found that, with proper care, even larger inventories are within reach. Our experiments show that accuracy only degrades slowly as the inventory increases, as long as we use training data of sufficient quality and in sufficient quantity.
Handwriting recognition can enhance user experience on mobile devices, particularly for Chinese input given the relative complexity of keyboard methods. Chinese handwriting recognition is uniquely challenging, due to the large size of the underlying character inventory. Unlike alphabet-based writing, which typically involves on the order of 100 symbols, the set of Hànzì characters in Chinese National Standard GB18030-2005 contains 27,533 entries, and many additional logographic characters are in use throughout Greater China.
For computational tractability, it is usual to focus on a restricted number of characters, deemed most representative of usage in daily life. Thus, the standard GB2312-80 set includes only 6,763 entries (3,755 and 3,008 characters in the level-1 and level-2 sets, respectively). The closely aligned character set used in the popular CASIA databases, built by the Institute of Automation of Chinese Academy of Sciences, comprises a total of 7,356 entries [6]. The SCUT-COUCH database has similar coverage [8].
These sets tend to reflect commonly used characters across the entire population of Chinese writers. At the individual user level, however, what is “commonly used” typically varies from one person to the next. Most people need at least a handful of characters deemed “infrequently written,” as they occur in, e.g., proper names relevant to them. Thus ideally Chinese handwriting recognition algorithms need to scale up to at least the level of GB18030-2005.
While early recognition algorithms mainly relied on structural methods based on individual stroke analysis, the need to achieve stroke-order independence later sparked interest into statistical methods using holistic shape information [5]. This obviously complicates large-inventory recognition, as correct character classification tends to get harder with the number of categories to disambiguate [3].
On Latin script tasks such as MNIST [4], convolutional neural networks (CNNs) soon emerged as the way to go [11]. Given a sufficient amount of training data, supplemented with synthesized samples as necessary, CNNs decidedly achieved state-of-the-art results [1], [10]. The number of categories in those studies, however, was very small (10).
When we started looking into the large-scale recognition of Chinese characters some time ago, CNNs seemed to be the obvious choice. But that approach required scaling up CNNs to a set of approximately 30,000 characters, while simultaneously maintaining real-time performance on embedded devices. This article focuses on the challenges involved in meeting expectations in terms of accuracy, character coverage, and robustness to writing styles.
We adopt in this work a general CNN architecture similar to that used in previous handwriting recognition experiments on the MNIST task (see, e.g., [1], [10]). The configuration of the overall system is illustrated in Fig. 1.
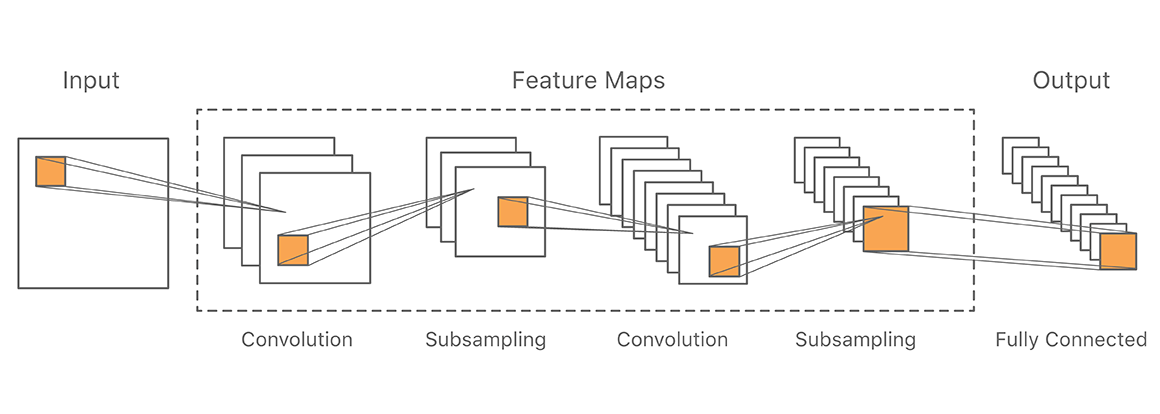
The input is a medium-resolution image (for performance reasons) of 48x48 pixels representing a Chinese handwritten character. We fed this input to a number of feature extraction layers alternating convolution and subsampling. The last feature extraction layer is connected to the output via a fully connected layer.
From one convolution layer to the next, we chose the size of the kernels and the number of feature maps so as to derive features of increasingly coarser granularity. We subsampled through a max-pooling layer [9] using a 2x2 kernel. The last feature layer typically comprises on the order of 1,000 small feature maps. Finally, the output layer has one node per class, e.g., 3,755 for the Hànzì level-1 subset of GB2312-80, and close to 30,000 when scaled up to the full inventory.
As baseline, we evaluated the previously described CNN implementation on the CASIA benchmark task [6]. While this task only covers Hànzì level-1 characters, there exist numerous reference results for character accuracy in the literature (e.g., in [7] and [14]). We used the same setup based on CASIA-OLHWDB, DB1.0-1.2, split in training and testing datasets [6], [7], yielding about one million training exemplars.
Note that, given our product focus, the goal was not to tune our system for the highest possible accuracy on CASIA. Instead our priorities were model size, evaluation speed, and user experience. We thus opted for a compact system that works real-time, across a wide variety of styles, and with high robustness towards non-standard stroke order. This led to an image-based recognition approach even though we evaluate on online datasets. As in [10], [11], we supplemented actual observations with suitable elastic deformations.
Table 1 shows the results using the CNN of Figure 1, where the abbreviation “Hz-1” refers to the Hànzì level-1 inventory (3,755 characters), and “CR(n)” denotes top-n character recognition accuracy. In addition to the commonly reported top-1 and top-10 accuracies, we also mention top-4 accuracy because, as our user interface was designed to show 4 character candidates, the top-4 accuracy is an important predictor of user experience in our system.
| Inventory | Training | CR(1) | CR(4) | CR(10) |
|---|---|---|---|---|
| Hz-1 | CASIA | 87.4% | 94.5% | 98.1% |
The figures in Table 1 compare with online results in [7] and [14] averaging roughly 93% for top-1 and 98% for top-10 accuracy. Thus, while our top-10 accuracy is in line with the literature, our top-1 accuracy is slightly lower. This has to be balanced, however, against a satisfactory top-4 accuracy, and perhaps even more importantly, a model size (1 MB) smaller than any comparable system in [7] and [14].
The system in Table 1 is trained only on CASIA data, and does not include any other training data. We were also interested in folding in additional training data collected in-house on iOS devices. This data covers a larger variety of styles (cf. next section) and comprises a lot more training instances per character. Table 2 reports our results, on the same test set with a 3,755-character inventory.
| Inventory | Training | CR(1) | CR(4) | CR(10) |
|---|---|---|---|---|
| Hz-1 | Augmented | 88.4% | 96.5% | 98.3% |
Though the resulting system has a much greater footprint (15 MB), accuracy only improves slightly (about 2% absolute for top-4 accuracy). This suggests that, by and large, most styles of characters appearing in the test set were already well-covered in the CASIA training set. It also indicates that there is no downside in folding more training data: the presence of additional styles is not deleterious to the underlying model.
Since the ideal set of “frequently written” characters varies from one user to the next, a large population of users requires an inventory of characters much larger than 3,755. Exactly which ones to select, however, is not entirely straightforward. Simplified Chinese characters defined with GB2312-80 and traditional Chinese characters defined with Big5, Big5E, and CNS 11643-92 cover a wide range (from 3,755 to 48,027 Hànzì characters). More recently came HKSCS-2008 with 4,568 extra characters, and even more with GB18030-2000.
We wanted to make sure that users are able to write their daily correspondence, in both simplified and traditional Chinese, as well as names, poems and other common markings, visual symbols, and emojis. We also wanted to support the Latin script for the occasional product or trade name with no transliteration. We followed Unicode as the prevailing international standard of character encoding, as it encapsulates almost all of the above mentioned standards. (Note that Unicode 7.0 can specify over 70,000 characters in its extensions B-D, with more being considered for inclusion). Our character recognition system thus focused on the Hànzì part of GB18030-2005, HKSCS-2008, Big5E, a core ASCII set, and a set of visual symbols and emojis, for a total of approximately 30,000 characters, which we felt represented the best compromise for most Chinese users.
After selecting the underlying character inventory, it is critical to sample the writing styles that users actually use. While there are formal clues as to what styles to expect (cf. [13]), there exist many regional variations, e.g., (i) the use of the U+2EBF (艹) radical, or (ii) the cursive U+56DB (四) vs. U+306E (の). Rendered fonts can also contribute to confusion as some users expect specific characters to be presented in a specific style. As a speedy input tends to drive toward cursive styles, it tends to increase ambiguity, e.g. between U+738B (王) and U+4E94 (五). Finally, increased internationalization sometimes introduces unexpected collisions: for example, U+4E8C (二), when cursively written, may conflict with the Latin characters “2” and “Z”.
Our rationale was to offer users the whole spectrum of possible input from printed to cursive to unconstrained writing [5]. To cover as many variants as possible, we sought data from writers from several regions in Greater China. We were surprised to find that most users have never seen many of the rarer characters. This unfamiliarity results in hesitations, stroke-order errors, and other distortions which we needed to take into account. We collected data from paid participants across various age groups, gender, and with a variety of educational backgrounds. The resulting handwritten data is unique in many ways: comprising several thousands users, written with a finger, not a stylus, on iOS devices, in small batches of data. One advantage is that the sampling of iOS devices results in a very clear handwritten signal.
We found a wide variety of writing styles. Figures 2-4 show some examples of the “flower” character U+82B1 (花), in printed, cursive, and unconstrained styles.



The fact that, in daily life, users often write quickly and unconstrained can lead to cursive variations that have a very dissimilar appearance. Conversely, sometimes it also leads to confusability between different characters. Figures 5-7 show some of the concrete examples we observe in our data. Note that it is especially important to have enough training material to distinguish cursive variations such as in Figure 7.



With the guiding principles discussed previously, we were able to collect tens of millions of character instances for our training data. Compare the 3,755-character system in the previous section with the results shows in Table 3, on the same test set, after increasing the number of recognizable characters from 3,755 to approximately 30,000.
| Inventory | CR(1) | CR(4) | CR(10) | Model Size |
|---|---|---|---|---|
| 30K | 85.6% | 95.2% | 97.5% | 15 MB |
Note that the model size remains the same, as the system of Table 2 was simply restricted to the “Hz-1” set of characters, but was otherwise identical. Accuracy drops marginally, which is to be expected, since the vastly increased coverage creates additional confusability of the kind mentioned earlier, for example “二” vs. “Z”.
Compare Tables 1-3 and you’ll see that multiplying coverage by a factor of 10 does not entail 10 times more errors, or 10 times more storage. In fact, as the model size goes up, the number of errors increases much more slowly. Thus, building a high-accuracy Chinese character recognition that covers 30,000 characters, instead of only 3,755, is possible and practical.
To get an idea of how the system performs across the entire set of 30,000 characters, we also evaluated it on a number of different test sets comprising all supported characters written in various styles. Table 4 lists the average results.
| Inventory | CR(1) | CR(4) | Model Size |
|---|---|---|---|
| 30K | 88.1% | 95.1% | 15 MB |
Of course, the results in Tables 3-4 are not directly comparable, since they were obtained on different test sets. Nonetheless, they show that top-1 and top-4 accuracies are in the same ballpark across the entire inventory of characters. This is a result of the largely balanced training regimen.
The total set of CJK characters in Unicode (currently around 75,000 [12]) could increase in the future, as the ideographic rapporteur group (IRG) keeps on suggesting new additions from a variety of sources. Admittedly, these character variants will be rare (e.g., used in historical names or poetry). Nevertheless, this is of high interest to every person whose name happens to contain one of those rare characters.
So, how well do we expect to handle larger inventories of characters in the future? The experiments discussed in this article support learning curves [2] based on training and test error rates with a varying amount of training data. We can therefore extrapolate asymptotic values, regarding both what our accuracy would look like with more training data, and how it would change with more characters to recognize.
For example, given the 10-times larger inventory and corresponding (less than) 2% drop in accuracy between Tables 1 and 3, we can extrapolate that with an inventory of 100,000 characters and a corresponding increase in training data, it would be realistic to achieve top-1 accuracies around 84%, and top-10 accuracies around 97% (with the same type of architecture).
In summary, building a high-accuracy handwriting recognition system which covers a large set of 30,000 Chinese characters is practical even on embedded devices. Furthermore, accuracy only degrades slowly as the inventory goes up, as long as training data of sufficient quality is available in sufficient quantity. This bodes well for the recognition of even larger character inventories in the future.
[1] D.C. Ciresan, U. Meier, L.M. Gambardella, and J. Schmidhuber, Convolutional Neural Network Committees For Handwritten Character Classification, in 11th Int. Conf. Document Analysis Recognition (ICDAR 2011), Beijing, China, Sept. 2011.
[2] C. Cortes, L.D. Jackel, S.A. Jolla, V. Vapnik, and J.S. Denker, Learning Curves: Asymptotic Values and Rate of Convergence, in Advances in Neural Information Processing Systems (NIPS 1993), Denver, pp. 327–334, Dec. 1993.
[3] G.E. Hinton and K.J. Lang, Shape Recognition and Illusory Conjunctions, in Proc. 9th Int. Joint Conf. Artificial Intelligence, Los Angeles, CA, pp. 252–259, 1985.
[4] Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner, Gradient– based Learning Applied to Document Recognition, Proc. IEEE, Vol. 86, No. 11, pp. 2278–2324, Nov. 1998.
[5] C.-L. Liu, S. Jaeger, and M. Nakagawa, Online Recognition of Chinese Characters: The State-of-the-Art, IEEE Trans. Pattern Analysis Machine Intelligence, Vol. 26, No. 2, pp. 198–213, Feb. 2004.
[6] C.-L. Liu, F. Yin, D.-H. Wang, and Q.-F. Wang, CASIA Online and Offline Chinese Handwriting Databases, in Proc. 11th Int. Conf. Document Analysis Recognition (ICDAR 2011), Beijing, China, Sept. 2011.
[7] C.-L. Liu, F. Yin, Q.-F. Wang, and D.-H.Wang, ICDAR 2011 Chinese Handwriting Recognition Competition,in 11th Int. Conf. Document Analysis Recognition (ICDAR 2011), Beijing, China, Sept. 2011.
[8] Y. Li, L. Jin , X. Zhu, T. Long, SCUT-COUCH2008: A Comprehensive Online Unconstrained Chinese Handwriting Dataset (ICFHR 2008), Montreal, pp. 165–170, Aug. 2008.
[9] K. Jarrett, K. Kavukcuoglu, M. Ranzato, and Y. LeCun, What is the Best Multi-stage Architecture for Object Recognition?, in Proc. IEEE Int. Conf. Computer Vision (ICCV09), Kyoto, Japan, Sept. 2009.
[10] U. Meier, D.C. Ciresan, L.M. Gambardella, and J. Schmidhuber, Better Digit Recognition with a Committee of Simple Neural Nets, in 11th Int. Conf. Document Analysis Recognition (ICDAR 2011), Beijing, China, Sept. 2011.
[11] P.Y. Simard, D. Steinkraus, and J.C. Platt, Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis, in 7th Int. Conf. Document Analysis Recognition (ICDAR 2003), Edinburgh, Scotland, Aug. 2003.
[12] Unicode, Chinese and Japanese, http://www.unicode.org/faq/han_cjk.html, 2015.
[13] F.F. Wang, Chinese Cursive Script: An Introduction to Handwriting in Chinese, Far Eastern Publications Series, New Haven, CT: Yale University Press, 1958.
[14] F. Yin, Q.-F. Wang, X.-Y. Xhang, and C.-L. Liu, ICDAR2013 Chinese Handwriting Recognition Competition, in 11th Int. Conf. Document Analysis Recognition (ICDAR 2013), Washington DC, USA, Sept. 2013.
Embedded Large-Scale Handwritten Chinese Character Recognition
April 13, 2020research area Computer Vision, research area Speech and Natural Language Processingconference ICASSP
As handwriting input becomes more prevalent, the large symbol inventory required to support Chinese handwriting recognition poses unique challenges. This paper describes how the Apple deep learning recognition system can accurately handle up to 30,000 Chinese characters while running in real-time across a range of mobile devices. To achieve acceptable accuracy, we paid particular attention to data collection conditions, representativeness of…
Language Identification from Very Short Strings
July 24, 2019research area Speech and Natural Language Processing
Many language-related tasks, such as entering text on your iPhone, discovering news articles you might enjoy, or finding out answers to questions you may have, are powered by language-specific natural language processing (NLP) models. To decide which model to invoke at a particular point in time, we must perform language identification (LID), often on the basis of limited evidence, namely a short character string. Performing reliable LID is more critical than ever as multi-lingual input is becoming more and more common across all Apple platforms. In most writing scripts — like Latin and Cyrillic, but also including Hanzi, Arabic, and others — strings composed of a few characters are often present in more than one language, making reliable identification challenging. In this article, we explore how we can improve LID accuracy by treating it as a sequence labeling problem at the character level, and using bi-directional long short-term memory (bi-LSTM) neural networks trained on short character sequences. We observed reductions in error rates varying from 15% to 60%, depending on the language, while achieving reductions in model size between 40% and 80% compared to previously shipping solutions. Thus the LSTM LID approach helped us identify language more correctly in features such as QuickType keyboards and Smart Responses, thereby leading to better auto-corrections, completions, and predictions, and ultimately a more satisfying user experience. It also made public APIs like the Natural Language framework more robust to multi-lingual environments.